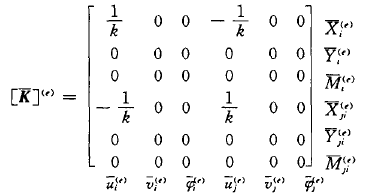空间梁拱组合体系桥梁是一种由拱肋、吊杆及桥面系纵、横梁组合共同受力的新型结构,由于它的结构轻盈、线形美观、桥面系建筑高度小等众多优点而在中、大跨桥梁,特别是在城市桥梁中广泛应用.这类桥型整体上可修建成外部静定体系,因此它可适用于各种地质条件,而其内部为超静定结构的特性使之内力计算较为复杂.对于这种桥梁结构的设计、分析,常以平面杆系有限元程序,结合具体的荷载横向分布系数综合计算,因而如何计算这类桥梁的荷载横向分布系数,成为解决问题的关键。
目前桥梁界普遍认为这种桥梁结构的横向分布按弹性支承连续梁的形式进行分布,但文献〔l〕里只对等跨等刚度连续梁的各种情况作了阐述,并制定了不同的表格供运用.由于空间梁拱组合体系桥梁常将机动车道、非机动车道及人行道做成分隔分道行驶的形式,横向不等跨及横梁刚度沿长度变化的现象比较突出.文中以嘉兴长纤塘桥的空间梁拱组合体系桥为背景,运用杆系有限元的基本原理,并借助弹簧刚度矩阵,提出了对于这种桥梁结构的荷载横向分布按弹性支承连续梁的精确解法,并用实桥试验结果进行了验证。
基本理论
1.1基本原理及计算图式
根据空间梁拱体系桥梁的组成特点,将空间梁拱组合式桥梁的计算通过荷载横向分布系数转化为平面梁拱结构,再利用杆系结构有限元理论将拱梁结构离散、并进行内力计算和分析.计算时,荷载横向分布计算采用的力学模式如图1.在这种力学模式中:认为每一梁拱拱片间的桥面系横梁为弹性支承在梁拱拱片上并且具有一定刚度的连续横梁,桥梁的荷载横向分布按弹性支承连续梁的形式进行分配。
1、2关于k值的计算
按弹性支承连续梁法计算荷载的横向分布系数关键在于弹簧刚度k值的确定.目前城市桥梁修建的空间梁拱体系桥梁常以三拱肋或四拱肋的形式出现,而且由于机动车道、非机动车道分道,边拱体系与中拱体系的整体刚度略有不同,故其k值应分别计算.根据弹簧刚度的定义k一F/汉式中:k为弹簧刚度;F为力;a为相应位移.在平面梁拱结构分析计算模型的跨中作用一单位力F根据弹簧的力学特性及杆系单元的模式,将弹簧单元的刚度矩阵写成与杆系单元相似的形式一1,利用杆系有限元程序分别求出每一梁拱体系中所求截面纵梁的竖向位移民,即可求出弹簧刚度k。
1.3关于弹簧刚度矩阵
为结合杆系有限元,这里引人弹簧单元,根据弹簧的性质推导出其单元的刚度矩阵如式(1)、(2),把这种单元的刚度矩阵加人到整体刚度矩阵中,按照杆系有限元的原理编制相应的程序,可计算任意条件下的弹性支承连续梁法计算荷载的横向分布系数(限于篇幅程序未列出)。
1)局部坐标系的弹簧单元刚度矩阵
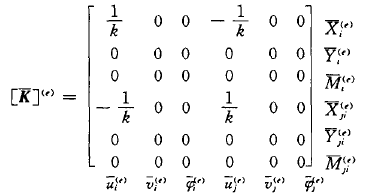
2)对应结构坐标系中的弹簧单元刚度矩阵
 2、试验研究
2、试验研究
为了解这类桥梁结构在实际荷载下的工作性能,验证文中提出的荷载横向分布理论及程序,结合嘉兴市长纤塘桥梁拱组合式桥梁的设计施工进行了试验研究,给出了理论计算值与试验测试值的比较。
2.1桥梁概况
长纤塘桥位于嘉兴市东升路,跨越长纤塘主河和支河,其中第一跨和第四跨上部结构采用52.44m及52.43m梁拱组合式桥梁,结构新颖,桥梁的设计荷载为汽一20级、挂一100,人群荷载3.5kN/mZ,桥面宽为15(机动车道)+2X2.0(分隔带)十2X6.5(非机动车道)十2x1.0(分隔带)+2x3.25(人行道)一40.50m,拱肋为钢管混凝土拱,横断面设4根长圆形拱肋,拱肋间设5道风撑,风撑采用直径600mm壁厚70mm钢管,桥面结构利用隔离带作为纵向加劲梁,并每隔5.20m设置一道横梁和柔性成品索吊杆挂于钢管混凝土拱肋上,纵向系梁及横梁均采用预应力混凝土结构,此外还在纵向系梁外的桥面板配置纵向预应力筋,预应力混凝土设计标号为C50,预应力材料采用奋15.24mm高强低松弛钢绞线,标准抗拉强度为Rb=1860MPa,OVM锚具,吊杆采用平行钢丝、墩头锚。
2.2荷载试验
2.2.1测试内容根据交通部颁布的试行办
法图及结构对称性,选取了该桥第四跨梁拱组合式桥梁进行重点观测和试验研究,同时第一跨跨中截面亦作为对比测试试验.测试内容主要为观察同一截面的不同拱肋、纵梁在各试验加载工况下的竖向位移,借以反应该桥梁的荷载横向分布工作性能。
2.2.2测试参数控制测试参数的控制是桥梁
测试的关键,而空间梁拱体系桥梁中拱片体系的受力计算关键在于荷载横向分布系数的计算.因此试验前的荷载横向分布系数计算采用了两种计算模式,以资比较。
1)第一种模式认为每一梁拱拱片间的横梁如同简支梁,桥梁的荷载横向分布按杠杆原理进行分配;
2)第二种模式认为每一梁拱拱片间的横梁具有一定的刚度、梁拱拱片为弹性支撑,桥梁的荷载横向分布按弹性支承连续梁的形式进行分第4期李新生等:空间梁拱组合体系桥梁的荷载横向分布计算9配,计算图式如图1所示。
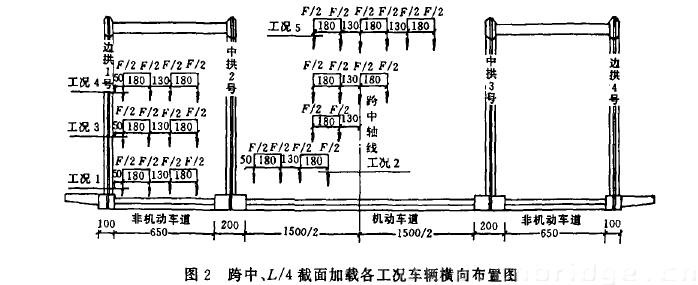
图2跨中、L4/截面加载各工况车辆横向布置图根据桥面系尺寸,机动车道按标准汽一20横向2列偏载、3列偏载、4列偏载、对称3列布置、挂车一100偏载和人群3.5kN/m“的方式,用上述两种计算模式、并乘以相应的车道折减系数,可以得到边拱肋、中拱肋的梁拱拱片的荷载横向分布系数和设计控制值,列于表1.表1两种力学假定模式的荷载横向分布系数表系数比较见图3所示。
从表1中可以看出:
(1)两种方法计算的汽车荷载的横向分布系数相差不是太大.对于边拱肋:方法1较大,方法2较小,其差值为0.041(约3.5%);而对于中拱肋差值为0.o49(约3写)。
(2)两种方法计算的人群荷载的横向分布系数边拱肋相差较大,差值为。.675(约18%),而中拱肋相差不大,差值只有。.223(约7%)。
(3)两种方法计算的挂车荷载的横向分布系数相差较大,差值为0.137(约20写).试验主要采用方法2的结果.试验中人群荷载根据内力等效原则用汽车模拟,加载的荷载横向分布系数最大理论控制值中拱肋为2.09,边拱肋为1.72,梁拱各截面的加载内力以此参数为高限。
2.2.3试验加载车辆横向布置试验加载车辆的横向布置见图.2
2.3横向分布试验结果
根据试验跨跨中截面的实测挠度值反算出加载各工况下各拱片体系的荷载横向分布系数与文中提出的弹性支承连续梁法计算的荷载横向分布。
2、3分析讨论
1)从图3中可以看出第一、第四跨跨中截面的横向分布实测曲线与文中提出的弹性支承连续一492.武汉理工大学学报〔交通科学与工程版)2001年第卷梁的计算值的分布曲线基本吻合,说明文中提出的算法的可靠性。
2)由于空间梁拱体系桥梁的横向连接大都以横梁作为主要承重结构,因此横梁的内力计算,必须按弹性支承连续梁进行计算和配筋,特别是对靠近中间拱肋支承附近的截面,往往由于弹性支承的影响,该处既表现为负弯矩控制该处截面上缘的设计,又表现为正弯矩控制该处截面下缘的设计,这一点值得桥梁设计者注意。
3)本试验没有对端横梁的荷载横向分布进行试验.但从定性上分析,对于端横梁应按连续梁或杠杆原理进行分配,从而在设计过程中应考虑荷载横向分布系数沿桥跨纵向的变化。
4)根据按弹性支承连续梁法和按杠杆原理法计算结果的对比可知,在实际工程的设计中,就从荷载的横向分布系数而言,可偏安全地采用杠杆原理法进行计算,但横梁的内力计算仍必需按弹性支承连续梁进行计算。
3、结束语
通过在杆系有限元程序中引人弹簧刚度矩阵,提出了分析空间梁拱组合体系桥梁荷载横向分布及其弹性支承上的连续横梁内力分析的弹性支承梁法,它能适用于桥面系横向不等跨变刚度弹性支承连续梁的荷载横向分布系数的计算,试验研究表明了本方法的可靠性。弹簧刚度k的计算值对于不同的截面、不同拱跨,其相应值亦不同.因此这种桥梁的荷载横向分布系数不仅表现为各梁拱结构横向的不同,而且沿跨长也是有变化的。
参考文献
胡肇滋.桥跨结构简化分析—荷载横向分布.北京:人民交通出版社,1996.78
项贻强.桥梁结构分析的数值方法及程序.北京:人民交通出版社,1993.112
交通部.公路桥涵设计规范.北京:人民交通出版社,1989.15
建设部.城市桥梁设计准则,CJJll一93.北京:中国建筑工业出版社,1997.18
(作者 李新生 申永刚 项贻强)