地震给人类社会的发展常常带来巨大损失,是人类面临的最严重自然灾害。桥梁工程作为生命线工程,其破坏不仅危害人们的生命财产安全,还往往给震后的抢险救灾工作带来巨大的困难。从几十年来世界各国发生的地震可见:1976年我国唐山地震,死亡人数约24万,重伤约16万,经济损失在100亿人民币以上,震害之严重为世界地震史所罕见。1989年美国洛马·普里埃塔地震,震级为M7.0。这只是一次中等强度的地震,却使城市高架桥严重损坏甚至部分倒塌,死亡人数62人, 经济损失为70亿美元。此次地震人员并无大量伤亡,但由于城市桥梁严重破坏,仍然导致了重大经济损失。1995年日本阪神地震给现代化的神户市造成了毁灭性的灾难。新干线、高速道路、高速铁路、高架桥的严重破坏,导致除航空外交通几乎全部切断,成为日本自1923年关东大地震以来人员伤亡最重、经济损失最大的一次破坏性地震。
最近几十年来,为了适应经济的发展需要,我国桥梁建设快速发展,尤其是近年来,各种形式的桥梁(如大跨度、超大跨度斜拉桥、悬索桥、拱桥及各种复杂的城市立交工程)的大量涌现,桥梁抗震设计中凸显了大量必须面对的众多问题。如何确保桥梁工程在地震过程中有足够的抗震能力和合理的安全度,减轻地震灾害带来的社会经济损失,成为工程界、学术界普遍关注的问题。
1.桥梁抗震分析方法
在与地震不断进行斗争的同时,人类对地震的研究也不断地获得进步。特别是近半个多世纪以来,人们对地震的破坏机理已有了日益深入的认识,并基于这种科学的认识而发展了各种抗震分析方法。
桥梁结构地震响应分析方法可以分为确定性方法和概率性方法两大类。确定性方法是以确定性的荷载作用于结构,求解该确定性荷载作用下结构动力反应的方法。概率性方法将地震作用视为随机过程,以此随机地震作用于结构,求出结构动力响应统计量。静力法、反应谱法和时程分析法均属于确定性方法。随机振动、虚拟激励法系列属于概率性方法。
1.1确定性抗震分析方法
1)静力法。静力法的概念是日本大房森吉在1900年提出的,此方法假设结构物各个部分与地震具有相同的振动,结构物上只作用着地面加速度乘以结构质量所产生的惯性力,惯性力具有与静力同样的性质,用等效静力作用于结构上,进行结构线弹性静力分析,计算其地震响应。静力法以地震荷载代替结构在地震强迫振动下的激励外因,作用于结构的计算静力效应代替结构在地面运动激励下的动力效应。从动力学的角度来看,把地震加速度看作结构地震破坏的的单一因素,静力法具有极大的局限性,它忽略了结构的动力特性这一重要因素,只有当结构物的基本固有周期比地面运动卓越周期小很多时,结构物在地震振动时才可能几乎不产生变形而可以被当作刚体,静力法才成立。不过,弹性静力法概念容易理解,计算简单,因此在实际工程应用中仍然受到欢迎。
非线形静力Pushover 分析方法——推倒分析方法。这种方法早在20世纪60年代末Pushover法就已经提出,最近几年来,Pushover法得到了较大的发展,并得到了广泛的应用。严格讲来Pushover法不能算作一种结构地震反应分析方法。但它提供了一个评估结构地震反应特别是非线形地震反应的简单而有效的方法,它能在一定程度上近似描述结构物在强震作用下的弹塑性反应性能,给出结构从屈服到极限状态的整个非弹性变形过程。这对于特殊、复杂的实际工程有较大价值。
Pushover分析方法是通过对结构施加单调递增侧向荷载来进行分析的一种非线形静力分析方法。该方法通常将相邻伸缩缝之间的桥梁结构当作空间独立框架考虑,上部结构通常假定为刚性。分析的初始阶段是对单独的排架墩在所考虑的方向上进行独立的倒塌分析,以获得构件在单调递增水平荷载作用下的整个破坏过程及变形特征。整个框架的分析将桥墩刚度模拟为非线形弹簧,计算出整个框架的初始刚度中心,施加单调递增的水平力, 并根据框架非线形发展的程度不断调整各个桥墩和结构的刚度,直到结构达到最终极限状态为止。
非线形PLLshov分析过程一般需要借助计算机程序完成。其基本假定为:①多自由度结构体系的响应与一等效单自由度体系相关,即结构响应主要由第一振型控制。②结构物沿高度变形的形状向量,在整个地震反应过程中保持不变。Pushover法实施步骤大致如下:①预先假定一个适当的、沿高度变化分布的侧向荷载模式;②确定与结构性能目标相对应的位移极值,如屈服位移、极限位移;③计算等效单 自由度体系的等效刚度和等效粘滞阻尼比;④逐渐增大荷载,计算结构特征荷载和特征位移之间相互关系曲线,也称能力曲线;⑤进行需求/能力比计算, 评估结构的抗震性能。 非线性 P u s h o v e r 法作为一种简单有效的性能评判方法,已被一些国家建筑设计规范引入。我国2001年颁布的《建筑抗震设计规范》(GB50011—2001)也将这种方法纳入。
2)反应谱理论。1943年M·A·Biot 提出了反应谱理论,并给出世界上第一条弹性反映谱曲线;1948年G·W·Honsner提出基于加速度反应谱曲线的弹性反应谱法;1956年N·M-Newmark率先把该法应用于抗震设计;1958年第一届世界地震工程会议后,被许多国家采纳并应用于工程结构抗震设计规范中。
反应谱方法的基本原理是:作用于结构的实际地震波是由含有一定卓越频率的复杂波组成, 当地震的卓越频率和结构的固有频率相一致时,结构物的动力反应就会变大。不同周期单自由度振子在某一地震记录激励下,可得到体系周期与绝对加速度、相对速度和相对位移的最大反应量之间的关系曲线,即加速度反应谱、速度反应谱和位移反应谱。由于客观存在的随机因素影响,使得不同地震记录得到的反应谱具有很大随机性、离散性,实际应用的规范反应谱是大量地震记录输入后得到众多反应谱曲线经统计平均和光滑后而得到的。
对于单自由度振子,其振动方程为:
上述振动方程的解用杜哈梅尔积分公式来表示:
对上式分别求一次和两次导数,可以得到单自由振子地震作用下的相对速度和绝对加速度反应的积分公式:
对于一般工程结构而言,其阻尼比较小,并且相位差也可以忽略不计。因此上面两式可以简化为:
由于地震加速度是不规则的函数,上述积分公式一般要通过数值积分的方法来求得反应的时程曲线。根据反应谱曲线,对于一个单自由度弹性体系,如果已知其自振周期和阻尼比,就可以从曲线中查得该体系在特定地震记录下的最大加速度。对于可以近似为单自由度体系规则的桥梁,其最大地震惯性力可以用相应的反应谱求出:
对于复杂的桥梁结构,无法直接利用单振型反应谱分析方法,而需要首先进行振型分解,其在单一水平方向地震作用下的动力平衡方程为:
必须假定结构的跨度不大,一致于结构所有节点均按同一加速度同相位运动。此方程用振型叠加法求解,可得:
结构的最大地震力:
目前采用的反应谱法对结构地震力采用弹性反应谱理论进行分析,反应谱法的最大缺点是假定结构是弹性状态。无法反应地震动持时和非线性的影响,原则上只适用于弹性结构体系。然而地震是一种随机荷载,一般允许结构在强烈地震中进入非线性状态。而对于多振型反应谱法,还存在振型组合的问题。尽管如此,因为弹性反应谱法通过反应谱概念将动力问题静力化,使得复杂问题变得简单易行,所以得到了广泛的应用。
3)时程分析法。时程分析法是根据选定的地震波或人工波,采用逐步积分的方法对动力方程进行直接积分,从而求得结构任意时刻地震反应的分析方法。
对于一个多自由度体系,采用有限元方法离散,得到体系的动力平衡方程:
边界条件为:
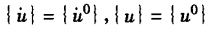
方程的计算方法一般有下列三类:①振型分析法:只适用于线性分析,即振动方程是二阶常系数微分方程,采用振型坐标对微分方程组解耦,使成为每个振型独立微分方程,然后对每个振型进行Dnhamel积分,一般可采用分段数值积分法。②直接积分法:不通过坐标变换,用数值积分法对线性或非线性地震振动方程求结构反应的时程解,常见的直接积分方法有中心差分法、线性加速度法、Wilson一0法、Newmark—a法和Houboltt法等。③增量平衡方程逐步积分法:将桥梁振动方程表示为时间间隔内的增量平衡方程,然后采用逐步迭代的数值分析求结构反应的时程解。
动态时程分析作为较为精确的结构动力分析方法,计算过程较为复杂,特别是对于大跨桥梁进行分析时,要考虑地震动输入、行波效应、土与地基基础相互影响和复杂地形对地震波的传播和散射的影响,准确模拟和计算桥梁结构的动力反应,都有一定的困难。
1.2概论性抗震分析方法
随机振动、虚拟激励法系列就属于概论性抗震分析方法。随机振动法假定地震动在时间和空间上都是随机变化的,采用空间相关函数来描述各点地震动的相关性。此方法是建立在各点地面运动的统计特征基础上,在确定了地震动的自功率谱和互功率谱后,计算出各反应量的统计规律。因为地震时地面运动就是一个随机场,所以随机振动分析方法日益受到重视。
对于大跨度桥梁结构,在进行抗震分析时应该考虑行波效应、部分相干效应和局部场地效应,传统的抗震方法在分析上遇到了困难,并且计算结果也和实际情况有较大差异。从上世纪五十年代起,在航天工程的工程振动研究中引入了概率和数理统计理论,极大地推动了对随机振动的研究。随机振动描述了客观存在的不确定性,在土木、机械、航空和航海等工程领域得到了广泛应用。经过几十年来国内外学者的共同努力,随机振动理论取得了丰硕的成果,已成为近代应用力学的一个重要分支。尽管作为其应用核心的线性随机振动基本理论早已成熟,然而这些理论成果在工程领域却远未得到充分应用;其原因是计算的复杂性和效率低下。
为了更好地把随机振动方法应用于工程实际,减少运算的工作量,几十年来,我国许多学者在随机振动的不同领域做了很多的研究工作,如林家浩等提出虚拟激励法系列。此方法可以使计算工作量大大减少。虚拟激励法主要特点是将平稳随机响应分析转化为简谐响应分析,将非平稳随机响应分析转化为确定性时间历程分析,从而可以用工程人员熟悉的确定性动力分析方法实现随机振动的求解。该法自动包含了全部参振振型之间的互相关项及全部随机激励之问的互相关项,计算的是各动力反应的统计规律,不受输入函数的制约,本质上是精确解法。
2.结束语
桥梁在地震作用下的动力计算是一个复杂的问题,尤其是对于大跨度的桥梁结构的抗震分析。经过多年的研究,桥梁结构的抗震分析方法已取得了长足的进步,本文主要介绍了桥梁抗震的主要分析方法,对工程中主要应用的反应谱法做了重点论述。