1 工程概况
衢江大桥主桥采用50m + 120m + 50mV 型刚构组合拱桥, 桥面宽30m , 结构型式立面图见图1。
1.1 主梁结构
主跨为跨径100m的单拱肋系杆拱结构,主梁为单箱双室预应力混凝土箱梁,梁高2.5m,顶板宽30m,底面宽10m,顶板厚28cm,底板及斜腹板厚25cm,中间腹板30cm。箱体两侧各布置4.5m悬臂结构,悬臂结构端部高0.18m,根部高0.6m。为减小主梁在温度变化时对V型结构产生较大的推力,主梁在拱趾处纵向断开,支承在拱趾与V型相交处的外伸的牛腿上。
边跨主梁为单箱4室断面,箱体两侧为4.5m悬挑结构。梁高2.5m,箱梁顶面全宽为30m,底面宽为10m,底板、斜腹板厚25cm,顶板厚30cm,两条中间腹板各厚30cm。
1.2 主跨拱肋
主跨拱肋为钢箱梁结构,箱体尺寸为2m×2m,板厚3.2cm,箱形内4个壁板上各布置3条纵向通长的T型肋,拱肋线形为二次抛物线( y = 21 x2/ 2500),矢跨比为1/ 4.76 ,拱固结于V型墩结构的斜腿顶部。
1.3 吊索及系杆拉索
吊杆按间距5m 均匀布置,每节吊索由两根高强度平行钢丝束构成, 吊索下端采用可调节锚头以便于在施工过程中通过吊索调整使拱肋及拱桥主梁的受力分配更加合理.系杆由高强度钢绞线构成,锚固于连接梁岸边侧的实体梁段内。
1.4 V 型墩
V 型墩由高5.95m的直墩和高9.91m的两条斜腿组成,下部直墩采用4m×10m矩形实体截面;上部斜腿为2m×10m的矩形实体截面,两斜腿顶部通过连接梁连接成为整体。
2.1 计算模型
计算模型按有限单元法建模,主梁、V 型墩和刚构均采用板单元,拱肋采用梁单元,吊杆和系杆用桁架单元。拱脚与V 型刚构内侧斜腿顶部刚连,计算模型处理为刚接点,中跨主梁由于在两拱趾附近处断开,支承在边跨主梁的牛腿上,模型处理为一端铰支、一端滑动的梁跨结构。系杆为高强钢绞线束组成,模型处理时,将它看作是一根与主梁重合的直杆单元。计算模型的边界条件为:两中墩底部为固定端,主梁两边跨端部为滑动支承。计算软件采用通用有限元分析软件ANSYS,板单元沿桥梁纵向、横向边长基本为1m,该模型节点总数为12 640 个,单元总数13 570 个。计算模型见图2。

2.2 计算荷载
恒载、二期恒载、活载、预加力等均在横截面上产生剪力滞效应,但其中恒载占主要地位,本文主要分析恒载与活载的剪力滞效应。
恒载包括自重、二期恒载、系杆预加力和吊杆预加力,其中自重根据结构的密度和体积由计算软件自动计算;二期恒载考虑了防护栏杆、铺装层、分隔带、人行道板以及过江管道的重量,综合考虑了上述因素,按线荷载84kN/ m计,均布加载在箱梁的顶板;系杆预加力通过给系杆一个初应变,该初应变产生初拉力35000kN;吊杆预加力通过预设初应变,产生初拉力2500kN。活载按城A级6车道加载,人群活载整体计算按3.0kN/ m2计算,局部计算按3.5kN/m2计算。活载根据所求截面内力影响线按最不利方式加载。
3 剪力滞产生机理
箱梁腹板传递的剪力流在腹板边缘的顶板应力要大一些,而向板内传递过程中,由于上下板会发生剪切变形,应力会逐渐变小,故实际上板的应力在横截面分布是不均匀的,呈现板的中间小而两边大的应力状态。剪力流在横向传递过程中有滞后现象,称为剪力滞后现象[1], 或剪力滞效应。剪力滞效应用剪力滞系数来表示,其表达式为

式中,λ为剪力滞系数;σ为实际截面的应力; 为初等梁理论的计算应力。
为初等梁理论的计算应力。
如果翼缘腹板处的正应力大于初等梁理论的计算值,称为正剪力滞,反之称为负剪力滞[2]。
本文在用有限元分析桥面板剪力滞效应时,采用的是板的中面应力,因为板的中面应力基本上反映了梁体整体弯曲的应力。计算剪力滞系数时,令

式中,σmax为箱梁顶板或底板单元中最大的中面正应力;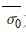 为相应箱梁顶板或底板单元中面应力的平均值,
为相应箱梁顶板或底板单元中面应力的平均值, 由下式给出
由下式给出

式中,σ0为板宽纵向的中面应力; y 为板宽方向;ly为板宽。
4 剪力滞效应分析
4.1 中跨跨中主梁剪力滞效应分析
(1) 中跨跨中主梁顶板剪力滞效应分析恒载和活载作用下中跨截面顶板中面的正应力分布如图3 、图4,剪力滞系数为1.248 和1.61
λ1/2=σmax/σ0= ( - 2.56) / ( - 2.05) = 1.248
λ1/2=σmax/σ0= ( - 2.0) / ( - 1.24) = 1.61
截面正应力沿宽度方向分布比较均匀,其分布的特点是中腹板处顶板的正应力最大,从中腹板到两侧翼缘板正应力渐渐减小。活载作用与恒载作用相比,活载在中跨主梁顶板上产生的正应力较小,截面上应力分布规律相同,但其剪力滞现象较为严重,剪力滞系数比恒载作用时要大得多。
(2) 中跨跨中主梁底板剪力滞效应分析
恒载和活载作用下中跨截面底板中面的正应力分布如图5、图6 ,其剪力滞系数为1.035和1.08
λ1/2=σmax/σ0= 5.58/ 5.39 = 1.035
λ1/2=σmax/σ0= 3.51/ 3.25 = 1.08
恒载作用下截面正应力沿宽度方向分布比较均匀,中腹板处的底板和两边腹板处底板的正应力较小,而中腹板和边腹板之间底板的正应力较大,即所谓负剪力滞现象[2]。
与恒载作用相比,活载在中跨主梁底板上产生的正应力分布的规律是不相同的,其特点是靠近腹板处底板的正应力数值较大,而远离腹板处底板的正应力较小。
4.2 边跨主梁剪力滞效应分析
主要对边跨跨中截面和边跨与Y型斜腿连接处即支点处的顶板和底板处的剪力滞效应进行分析。
4.2.1 边跨跨中主梁剪力滞效应分析
(1) 边跨跨中主梁顶板剪力滞效应分析
恒载和活载作用下边跨跨中截面处的顶板中面正应力分布如图7和图8,其剪力滞系数分别为1.66 和1.46。
λ1/2=σmax/σ0= ( - 3.73) / ( - 2.25) = 1.66
活载作用下顶板的剪力滞系数小于恒载引起的剪力滞系数。
(2) 边跨跨中主梁底板剪力滞效应分析
边跨跨中截面处的主梁底板中面正应力在恒载和活载作用下分布如图9和图10,其剪力滞系数分别为1.105 和1.12。
λ
1/2=σ
max/σ
0= 5.93/ 5.37 = 1.105
边跨跨中主梁底板的剪力滞的特点是两边腹板处正应力大而中腹板处小, 变化幅度不大。
4.2.2 边跨支点处主梁剪力滞效应分析
(1) 边跨支点处主梁顶板剪力滞效应分析
恒载和活载作用下边跨支点处主梁顶板中面正应力如图11、图12,剪力滞系数为1.988 和2。
λ0=σmax/σ0= 10.3/ 5.18 = 1.988
λ0=σmax/σ0= 1.4/ 0.71 = 2
边跨和V型斜腿相交处剪力滞现象最为突出,其剪力滞系数高达2,设计时应引起足够的重视。
(2) 边跨支点处主梁底板剪力滞效应分析
恒载和活载作用下边跨支点处主梁底板中面正应力如图13 、图14 ,剪力滞系数为1.388 和1.38。
边跨支点处主梁底板的剪力滞的特点是两边腹板处正应力大而中腹板处小,变化幅度比顶板小,但其剪力滞系数为1.388 ,比跨中大得多。
4.3 剪力滞系数分布
根据以上分析,将不同荷载作用下主梁沿桥梁长度方向不同截面的剪力滞系数用图15表示如下:
5 结论
通过计算分析,衢江大桥主梁剪力滞现象有以下特点:
(1) 底板由于没有悬臂板部分, 截面纵向应力分布比较均匀,纵向应力最大值在边腹板处,剪力滞系数都比顶板小;顶板纵向正应力最大值一般在中腹板处,剪力滞系数都比较大。吊杆的预拉力会影响顶板截面的纵向应力分布,一般是使中腹板处顶板的纵向应力最大值减小。
(2) 中跨主梁的使用应力很小,虽然存在剪力滞现象,但对设计来说,影响并不大。
(3) 边跨主梁工作应力较大,特别是边跨主梁与V型腿相交处是强度控制截面,而且边跨主梁剪力滞后现象严重, 剪力滞系数高达2.0 ,设计时必须予以特别的注意。
参考文献:
[1 ] 项海帆.高等桥梁结构理论[M] .北京: 人民交通出版社,2001.
[2 ] 罗旗帜.变截面箱梁的负剪力滞[J ] .重庆交通学院学报,1997 ,16 (3) .




 为初等梁理论的计算应力。
为初等梁理论的计算应力。
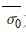 为相应箱梁顶板或底板单元中面应力的平均值,
为相应箱梁顶板或底板单元中面应力的平均值, 由下式给出
由下式给出










