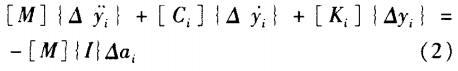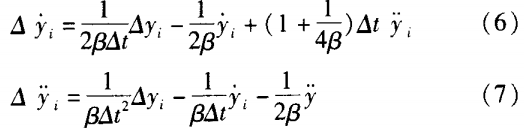《铁路工程抗震设计规范》明确规定:混凝土连续梁主跨大于等于80m桥梁为特别重要桥梁,在多遇地震作用下要进行强度及稳定性验算;罕遇地震作用下应按非线性时程反应分析法进行延性验算。我国《铁路工程抗震设计规范》与日本道路协会关于桥梁抗震的规定相比,在延性分析时所采用的计算方法和计算模型方面没有明确规定,且对于地震作用下桥墩的抗剪性能评价也没有提及。国内诸多学者对连续梁桥二级设防两阶段设计理念、支座摩擦力对连续梁抗震性能的影响、连续梁桥横桥向地震反应分析、大跨度连续梁桥地震反应分析等进行了多方面的研究。本文在已有的研究基础上,以一座(48+80+48)m铁路连续梁桥为工程背景,使用通用有限元软件和自编程序,按《铁路工程抗震设计规范》中三水准抗震设计要求,进行了多遇地震弹性和罕遇地震弹塑性地震反应分析及相应抗震性能评价。进一步明确了连续梁桥抗震验算方法,弥补了规范的不足。
1. 动力方程的求解
结构在地震作用下的运动方程为:
当结构为线弹性时,结构的刚度保持不变,此时方程(1) 的求算方法有3类:时域分析法、频域分析法和振型叠加法;当结构进入弹塑性后,结构的刚度发生了改变,采用(1) 式的增量形式进行分段线性逐步积分求解,第i步的增量方程见式(2) :
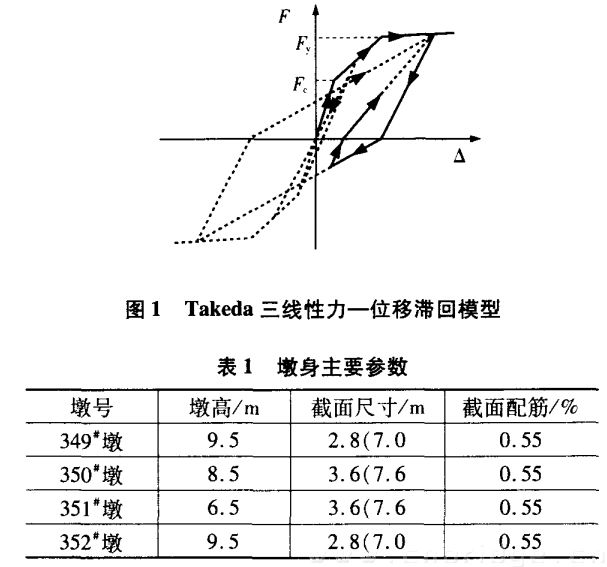
式(2)常用的求解方法有Wilson—0法和Newmark—JB法,二者的求解步骤基本相同,均需在求解的过程中,依据恢复力曲线模型来确定单元刚度矩阵。常用的钢筋混凝土恢复力曲线模型有Clough双线性和Takeda三线性模型(图1)。当采用Newmark一法求解时,第i步的增量位移可由下式求出:
第i步的增量速度和增量加速度可分别由以下计算式求出:
2.工程概况及计算模型
某铁路双线三跨(48+80+48)m连续梁,桥墩为圆端形截面,纵向钢筋的全截面配筋率为0.5%,其中351号墩为固定墩,各桥墩的详细尺寸如表1所示。安全评估报告提供该桥50年超越概率为63.2%的场地地面峰值加速度为0.05g,50年超越概率为2%的场地地面峰值加速度为0.34g。
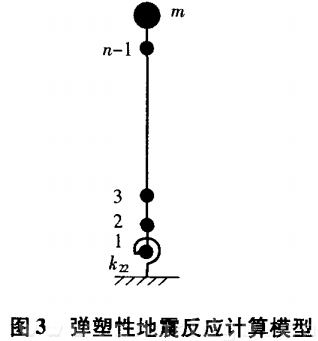
弹性地震反应计算时采用三维有限元方法建立桥梁的计算力学模型,如图2所示。计算模型中,地基对结构的约束作用简化成平动弹簧和转动弹簧,刚度弹簧可按m法计算。弹塑性地震反应时,固定墩顺、横桥向采用平面杆系有限元计算模型,如图3所示。地基对结构的约束作用以一个转动弹簧来模拟,为作用于墩顶的集中质量,顺桥向为全部桥跨质量,横桥向为固定墩相邻跨质量的一半和墩身质量,为转动弹簧刚度,1,2,3 …,n为节点号。
3. 地震反应分析
弹性地震反应分析时,分别进行了反应谱和时程地震反应分析;弹塑性地震反应分析时,采用集中质量矩阵,瑞利阻尼和Takeda三线性恢复力模型,输入墩顶力一位移骨架曲线,等效塑性铰长度取墩底截面的计算方向高度。
3.1 弹性地震反应分析
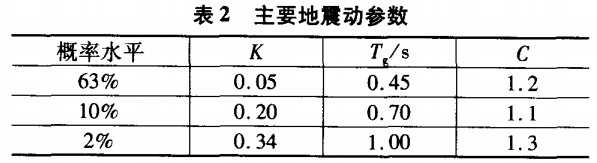
反应谱计算时,取前600阶振型进行叠加,安评报告提供的设计加速度反应谱(T) 的计算公式见式(8),主要地震动参数如表2所示。
式(8)中T1、T2为反应谱拐点周期,βm为动力放大系数,c为衰减系数,T小于0.04S时,取动力放大系数β(T)=1.0 。主要地震动参数列于表2,Ts为特征周期,为地震系数。
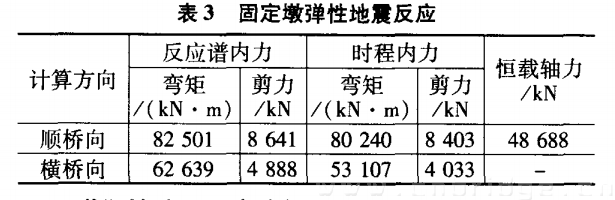
固定墩的弹性地震反应计算结果如表3所示,表中时程内力为输入3条地震波下最大值的平均。
3.2 弹塑性地震反应分析
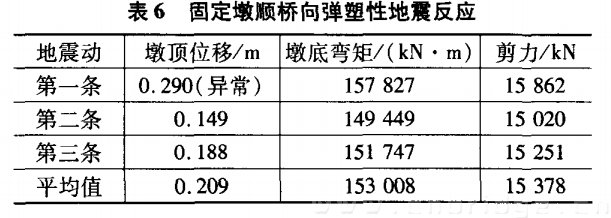
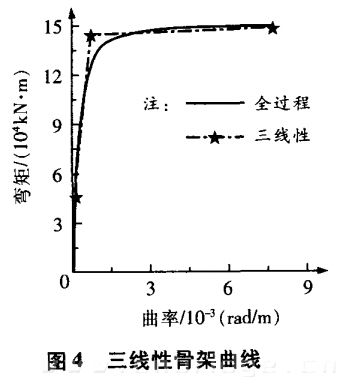
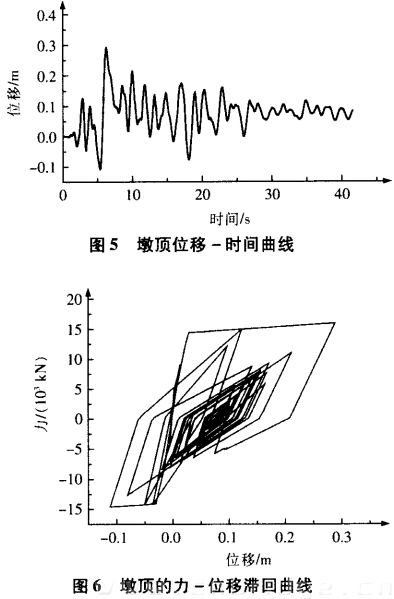
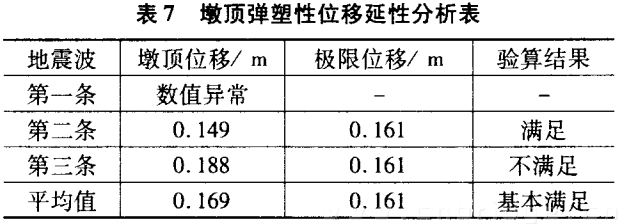
根据钢筋和混凝土的应力一应变关系,采用条带法可求得固定墩的弯矩一曲率全过程曲线J,依据等能量法由全过程曲线来确定三线性骨架曲线,计算结果列于表4及示于图4 。假定曲率沿墩身的分布,可由墩底的三线性弯矩曲率骨架曲线求得墩顶的三线性力一位移曲线,计算结果如表5所示。由于固定墩横桥向尺寸与墩高尺寸相差不大, 罕遇地震下不再进行延性验算。50年基准期2%超越概率水平下,固定墩顺桥向弹塑性地震反应如表6和图5 、图6所示。
4. 抗震性能评价
4.1 多遇地震强度验算
取表3中的反应谱控制内力进行强度验算。横桥向的计算偏心e:62639/48688=1.29m小于规范允许偏心[e]=2.66(0.7×7.6/2)m;顺桥向的计算偏心e:82501/48688=1.69m大于规范允许偏心[e]:1.26(0.7×3.6/2)m,应进行应力验算。按钢筋混凝土结构考虑应力重分布进行应力验算,混凝土的最大压应力为10.2MPa;钢筋的最大拉应力为186.0MPa。满足设计强度要求,可达到“小震不坏”的抗震设防要求。
4.2 罕遇地震延性验算
取表6中弹塑性分析结果进行延性验算,第一条地震波下墩顶的位移远比其它两条的值大( 是第二条的2倍) ,属异常数据,仅作参考,不作为依据。由表7 知,该桥基本满足延性要求。
4.3 横桥向抗剪能力验算
4.3.1 墩柱抗剪强度估算
Priestley等人认为钢筋混凝土墩柱的剪切强度由三部分组成,可表示为:
在本文算例中,固定墩横桥向尺寸为7.6m,墩高为6.5m,计算横桥向抗剪强度时,视桥墩为弹性状态,此时取0.29,Vp的贡献暂不计入。经计算得墩柱抗剪强度V=27 401kN。
4.3.2 抗剪能力验算
由表8可见,多遇地震下,抗剪强度满足“小震不坏”的设防要求,但是,罕遇地震下抗剪能力稍有不足,应加强设计。
5 . 结论
本文以一座双线三跨铁路连续梁桥为工程背景,按照《铁路工程抗震设计规范》中三水准抗震设计要求,采用通用有限元软件和自编程序对目前铁路客运专线常用的连续梁桥进行了详细的地震反应分析及全面的抗震性能评价,明确了铁路连续梁桥抗震验算方法,弥补了《铁路工程抗震设计规范》计算方法不能详细反映此类桥梁抗震性能的不足,为铁路连续梁桥抗震性能评价和抗震设计提供了理论基础。