随着交通量的日益增加,桥梁必须具有更宽的桥面和更多的车道才能满足通行需求.然而诸多力学方面的难题限制了桥面宽度,比如桥面太宽将导致主梁横向弯矩过大,畸变和剪力滞问题严重,而且从美学因素考虑,桥面宽度也不宜过大,因此,一般单幅桥梁桥面宽度在40m左右,容纳8个车道.此外,为了增大既有桥梁的通行能力,实际工程中经常会在其附近新建一座类似桥梁,从而构成平行双幅桥梁,平行双幅桥可分为两类:第一类是同时新建的平行双幅桥,第二类是对已有桥梁扩建从而构成的平行双幅桥。
近年来,平行双幅桥以其更大的通行能力越来越多地被设计应用,如美国的FredHartman大桥和Tacoma大桥,日本的尾道大桥和名港西大桥以及我国广东省佛山市平胜大桥和山东省青岛海湾红岛航道桥等等.然而由于平行双幅桥桥面距离较近,气流流经时会在上、下风侧桥面之间产生复杂的气动干扰效应,可能对大桥的静力和动力抗风性能产生显著影响。为此,Akihiro Honda对三幅相互平行的连续箱梁桥进行了气动稳定性研究,结果表明桥面之间的气动干扰对桥梁的静动力特性都有明显影响。Sarkar 在1994年也对平行双幅桥颤振性能进行了研究,研究表明均匀流场中气动干扰效应对颤振导数稍有影响,紊流场中影响很小,但是Sarkar研究的平行双幅桥桥面间距过大,气动干扰效应可能已不明显。2005年Irwin对新老Tacoma大桥气动干扰效应进行了研究并指出两桥之间的气动干扰效应几乎可以忽略,但由于新、老Tacoma大桥桥面之间距离较远,且主梁为透风较好的桁架梁,因而气动干扰效应不明显。在此之后,Kimura以及我国学者陈政清等也对平行双幅桥的气动干扰效应做了一定程度的研究,研究表明气动干扰效应与桥面间距和来流风向有关,并且气动干扰效应引起的振动响应十分复杂,在进行振动响应研究时不可忽略。
本文以天津塘沽海河既有独塔斜拉桥拓宽工程的初步设计方案为背景,基于一系列弹簧悬挂节段模型风洞试验,着重介绍箱形分离平行双幅桥面之间气动干扰效应对成桥状态颤振稳定性和涡振特性影响的研究结果。
1.工程背景及试验概况
如图1和图2所示,已建成的天津塘沽海河大桥(以下简称既有桥)为一座独塔双索面混合斜拉桥,全长500m,其中主跨为总长310m的分离双箱钢箱梁,边跨为总长190m的分离双箱混凝土箱梁,桥面宽度(B)为23m,主梁高为3 m,拓宽扩建中新桥(以下简称新建桥) 与既有桥呈对称分布,主跨仍为310m,边跨220m,主梁标准截面形式及沿纵桥向分布与既有桥类似,两幅桥轴线距离为35m,桥面净距离(D)为12m即D/B=0.52,既有桥和新建桥均为混合斜拉桥,主跨均为分离双箱钢箱梁,边跨为预应力混凝土箱梁。
颤振和涡激共振节段模型风洞试验均在同济大学TJ一2大气边界层风洞中进行,该风洞的试验段尺寸为3.0(宽)×2.5(高)×15.0m(长),风洞可达到的最大风速为68m/s 。
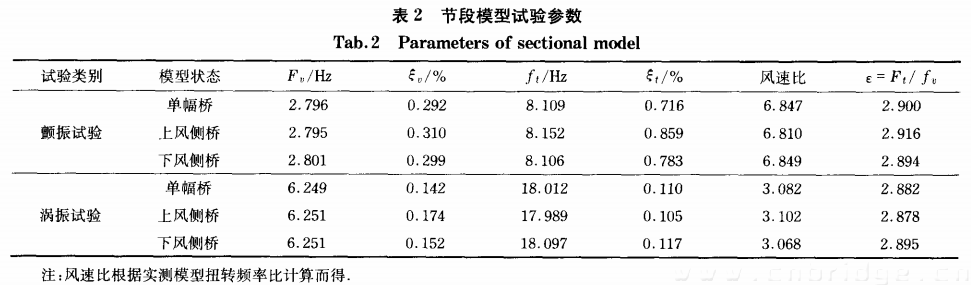
颤振和涡激共振的节段模型试验中主梁外形以以主跨钢箱梁标准断面为模拟对象,用于模型设计的实桥基本参数如表l所示,其中质量和质量惯矩考虑了全桥振动和空间振动效应.模型的几何缩尺比取为1/50,单幅桥模型主梁宽度为0.460m,高度为0.060m.刚体节段模型的骨架由金属构成,金属框架长1.700m,桥面用三夹板和豪适板( 高密度泡沫塑料板) 来模拟以保证外形的几何相似性,检修车轨道、检修道护栏及防撞栏用ABS塑料板由电脑雕刻制成。
既有桥和新建桥的二元刚体节段模型均用8根弹簧悬挂在风洞中,如图3,4所示,两者的相对位置与实桥相似。在颤振试验中,为了尽可能地获得颤振临界风速,需要采用较小的风速比,故所用弹簧刚度相应也较小。但在涡激共振试验中,涡振发生风速相对颤振临界风速要低得多,因此,为了提高风速的分辨率,需要采用比颤振试验更大的风速比,相应的弹簧刚度较颤振试验的大。试验中,可以通过调节悬挂弹簧的前后丝杆的相对高度来改变模型姿势,从而模拟上、下风侧桥正负风攻角状况,其中图5即为3度风攻角的试验工况.采用加速度传感器来测量节段模型的风振响应。为了研究气动干扰效应对其上风侧和下风侧颤振稳定性和涡振性能的影响,这里分别进行了单幅桥和双幅桥两种结构状态下的试验,其中,双幅桥试验中同时对上、下风侧两个梁进行加速度响应测量,模型试验的参数如表2所示。
2.气动干扰效应对颤振性能影响研究
2.1气动干扰效应对颤振临界风速的影响
单、双幅桥面的颤振试验风速均为1-20m/s ,临界风速试验结果如表3 所示。结果显示:当风攻角为3度时,在试验风速范围内单幅桥和双幅桥的上、下风侧桥均发生了竖弯和扭转耦合颤振,其中,上风侧桥和下风侧桥的颤振临界风速分别比单幅桥的颤振临界风速下降15.0%和17.0%,而下风侧桥的颤振临界风速又比上风侧桥的颤振临界风速低了2.3%。
当风攻角为0度时,在试验风速范围内双幅桥的上、下风侧桥均发生了颤振,单幅桥未发生颤振并且其扭转阻尼比还处于上升阶段.下风侧桥的颤振临界风速比上风侧桥的颤振临界风速低了9.4%。
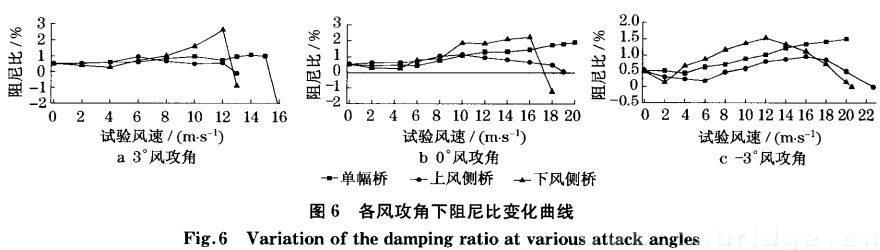
当风攻角为-3度时,在试验风速范围内,单幅桥和双幅桥的上、下风侧桥都没有发生颤振,且单幅桥的扭转阻尼比还处于上升阶段,但上、下风侧桥的阻尼比均已进入衰减阶段,并且下风侧桥比上风侧桥的阻尼比衰减快,因此,双幅桥比单幅桥颤振临界风速低,下风侧桥又比上风侧桥颤振临界风速低.延长上、下风侧桥的阻尼比曲线( 如图6所示) 可预测其颤振临界风速(见表3),由此可知,下风侧桥的颤振临界风速比上风侧桥的颤振临界风速低约9.3%。
综上所述,由于双幅桥之间的气动干扰效应,结构相同、横向间距较小的上、下风侧两座桥梁的颤振稳定性均要明显差于相同结构单幅桥的颤振稳定性,而且下风侧桥梁的颤振稳定性最差.因此,在对既有桥梁拓宽扩建时有必要考虑双幅桥之间的气动干扰效应,检验双幅桥状态下既有桥和新建桥是否仍然满足颤振稳定性要求。
2.2 气动干扰效应对气动导数的影响
为了研究气动干扰效应对平行双幅桥气动导数的影响,利用自由衰减振动法和同济大学丁泉顺博士基于改进最小二乘法提出的气动导数识别方法,提取了单、双幅桥的气动导数进行比较.双幅桥气动导数识别时上、下风侧桥面模型都按二元弹性状态悬挂于风洞中,两模型参数与颤振临界风速测试时完全一致,提取上风侧桥气动导数时,对上风侧桥面进行脉冲激励使之在风场中自由衰减,而下风侧桥面则保持自然振动状态,下风侧桥气动导数识别时则反之。由此得出各风攻角下单、双幅桥气动导数变化曲线如图7所示。
由图7可知,当风攻角为0度时,双幅桥的上风侧桥与单幅桥的气动导数随着折减风速增加的变化趋势接近,在试验的折减风速(U/fB) 范围内仍处于下降状态;而对于双幅桥的下风侧桥梁,虽然在低折减风速(U/fB<3)时其曲线与单幅桥的接近,但在U/fB=3附近出现转折点,随U/fB的增加开始由递减变为递增,并在U/fB=5.5附近由负变为正, 开始提供气动负阻尼.由此可知,0攻角时,气动干扰效应对上风侧桥的气动导数影响不是很明显,而对下风侧桥的气动导数影响较大,其气动导数转折点较大幅度地提前, 这可能是上、下风侧桥振动产生的紊流对顺风向影响较大,而对逆风向影响较小的缘故.3度风攻角时,双幅桥的上风侧桥与单幅桥的气动导数随着U/fB增加的变化趋势与0度风攻角时的情况相似,在试验的U/fB范围内仍处于下降状态,但双幅桥的上风侧桥的A 曲线的下降速度更快.然而,上风侧桥的A 曲线在U/fB=4.0附近下降速度突然变慢,接近于变为上升趋势的转折点.双幅桥下风侧桥曲线的变化趋势与其在0。攻角时的情况类似,但转折点出现的更早,在U/fB=2附近,并且在U/fB=3.5附近由负变为正,开始提供气动负阻尼。由此可知, 3度风攻角时,气动干扰效应使得上、下风侧桥的曲线均较早地出现了从下降到上升的转折点,而且下风侧桥的曲线转折点出现得更早。
-3度风攻角时,在试验风速范围内三种工况下气动导数的变化趋势比较接近,但双幅桥的上、下风侧桥的A 曲线末端(U/fB=5~6) 已开始呈现明显得处上升趋势,其中上风侧桥曲线的上升趋势更明显.由此可见,-3度风攻角时在低风速区,两幅桥的气动干扰效应对气动导数影响相对其它两个风攻角时的影响要小。
3.气动干扰效应对涡激共振影响研究
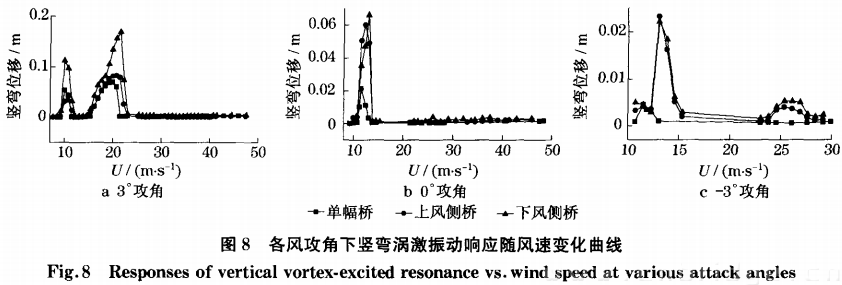
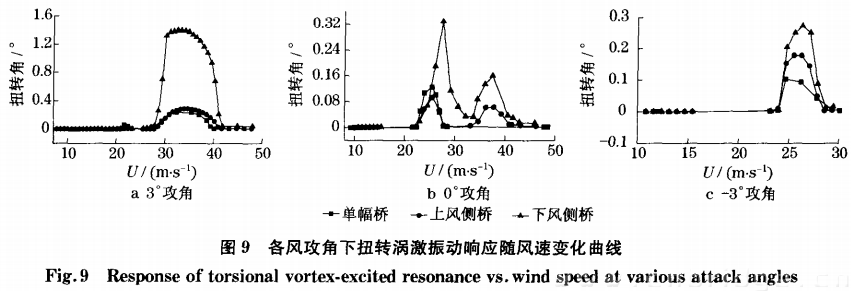
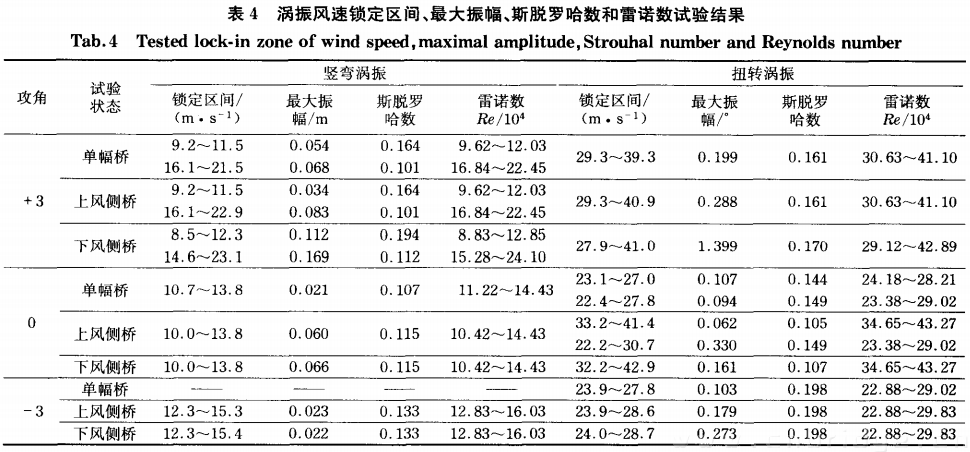
试验中,双幅桥的上、下风侧桥均发生了竖弯和扭转涡激共振,并且与单幅桥的涡振特性有较大差别。试验所得的单幅桥和双幅桥上、下风侧桥的竖弯和扭转涡振响应随风速变化曲线如图8,9所示,相应的涡振风速锁定区间、最大振幅、斯脱罗哈数等结果如表4所示。下面将通过考察表征涡激共振特性的三个重要特征参数(最大振幅、锁定风速区间以及斯脱罗哈数) 来讨论平行双幅桥之间的气动干扰效应对其涡激共振特性的影响规律。
3.1 气动干扰效应对涡振振幅的影响
由表4和图8可见,0度风攻角时单幅桥竖弯涡振振幅最大值为0.021m,振幅相对较小,并小于按规范公式计算的竖弯涡振允许振幅0.104m,双幅桥的上、下风侧桥的竖弯涡振最大振幅为0.060m和0.066m,分别为单幅桥振幅的2.82倍和3.10倍,并且下风侧桥要比上风侧桥的振幅高;3度风攻角时单、双幅桥试验均分别发生了两次竖弯振,单幅桥的竖弯涡振振幅最大值为0.068m,双幅桥的上、下风侧桥的竖弯涡振最大振幅分别为0.083m和0.169m,分别为单幅桥振幅的1.21倍和2.45倍,其中下风侧桥两 次竖弯涡振最大振幅均已超过竖弯涡振允许振幅;-3度风攻角时,单幅桥未发生明显的涡振现象,但双幅桥时上、下风侧桥均出现了振幅较小的竖弯涡振.综上所述,气动干扰效应对平行双幅桥下风侧桥的涡振振幅影响比对上风侧桥的涡振振幅影响更大,同时3度仍然为发生涡振的最不利风攻角。
试验过程中也明显看出下风侧桥比上风侧桥涡振振幅大,这可能是因为上风侧桥振动对其尾流会产生显著的横向扰动,这种扰动引起的旋涡或周期性交变气动力又将扩散和传递至其下风侧区域,并对下风侧桥产生直接的附加作用力,从而使其涡振振幅大幅度增加.而下风侧桥的振动虽然也会对周围流场产生扰动,但这种扰动引起的旋涡或周期性交变气动力也将扩散和传递至其下风侧区域,但其对处于逆风向的上风侧桥的作用应该主要是通过波动的形式传递,因此对其振幅影响相对较小.由表4和图9可见, 0度风攻角时,单幅桥状态扭转涡振只发生了一次,但双幅桥状态下上、下风侧桥均发生了两次扭转涡振.单幅桥扭转涡振振幅最大值为0.10,振幅较小,并小于按规范公式 计算的扭转涡振振幅允许值0 .183度.双幅桥的上、下风侧桥的扭转涡振最大振幅分别为0.094度和0.330度,分别为单幅桥振幅的0.87倍和3.06倍,并且下风侧桥的最大振幅已明显超过了扭转涡振允许振幅.3风攻角时,单幅桥扭转涡振最大振幅为0.199度,双幅桥中上、下风侧桥的扭转涡振最大振幅分别为0.288度和1.399度,分别为单幅桥振幅的1.45倍和7.03倍,并均大于扭转涡振允许振幅.-3度风攻角时,单幅桥扭转涡振最大振幅为0.103度,双幅桥的上、下风侧桥的扭转涡振最大振幅分别为0.179度和0.273度,分别为单幅桥振幅的1.74倍和2.65倍 。
试验结果表明, 平行双幅桥的气动干扰效对扭转涡振振幅的影响十分明显,相比于对竖向涡振的影响,扭转涡振振幅增大幅度更加显著.其原因首先在于上、下风侧两幅桥之间的透风槽区域是流动干扰和交换的最主要部位,因此气动干扰产生的附加气动力对下风侧桥梁的上游风嘴和上风侧桥梁的下游风嘴这两处离开各自扭转轴较远的部位的作用最直接也较强,从而产生较大的附加交变扭矩,引起较大的扭转涡振.另一个可能的原因是气动干扰效应对平行双幅桥涡振振幅的影响程度应该与桥面振动程度有关, 桥面振动越强烈,两桥之间的气动干扰效应越明显。
3 .2 气动干扰效应涡振风速锁定区间和斯脱罗哈数的影响
由表4可知,各工况的斯脱罗哈数均在0.1~0.2范围内,而雷诺数也在10左右.3度风攻角时,平行双幅桥上风侧桥与单幅桥的竖弯涡振和扭转涡振风速锁定区间基本相同,并且斯脱罗哈数也保持一致.与单幅桥相比,下风侧桥的竖弯和扭转涡振的起振风速要低,风速锁定区间要分别长57%~65%和31%左右,斯脱罗哈数要分别高出11 %~18 %和6%。
0度风攻角时,平行双幅桥的上、下风侧桥的竖向涡振起振风速、风速锁定区间和斯脱罗哈数相同,并且与单幅桥相比,起振风速均略低,风速锁定区间要长23%.对于扭转涡振,平行双幅桥的上、下风侧桥均在两个风速区间出现涡激共振,且下风侧桥的起振风速略低、斯脱罗哈数略高,下风侧桥的两个风速锁定区间比上风侧桥的分别要长 57%和30%.而此时,单幅桥只在其中的一个较低风速区问出现涡激共振.在这个较低的风速锁定区间,与单幅桥相比,双幅桥的上、下风侧桥的起振风速略高,斯脱罗哈数均要低3%左右,风速锁定区间分别要长38%和118%。
-3度风攻角时,单幅桥没有发生明显的竖向涡激共振,而双幅桥的上、下风侧桥均出现的小振幅竖向涡激共振,且它们的起振风速、风速锁定区间和斯脱罗哈数基本相同.对于扭转涡振,单幅桥和双幅桥的上、下风侧桥均在一个风速区间发生和涡激共振,三者的起振风速、斯脱罗哈数基本相同,双幅桥的上、下风侧桥的涡振风速锁定区问基本一致,并比单幅桥的长21%左右。
综上所述,与单幅桥相比,平行双幅桥的上、下风侧桥的涡振风速锁定区间均要长,起振风速低,斯脱罗哈数大,发生涡激共振的风速区间数可能也要多,因此发生涡振可能性也更大.而在平行双幅桥中,与上风侧桥相比,下风侧桥的涡振起振风速一般不会高,尤其是在3度风攻角情况下,其起振风速明显要低,相应的斯脱罗哈数明显要高,风速锁定区间明显要长,发生涡激共振的概率也明显要高.这可能是因为上风侧桥的振动对下风侧桥产生的拍振作用较大,迫使下风侧桥在更低和更高的风速下发生涡振;而下风侧桥振动引起的拍振作用对上风侧桥的影响由于平均风的作用而减小。
4.结论
通过单幅桥和平行双幅桥的节段模型测振对比风洞试验,对箱形平行双幅桥之问的气动干扰效应作用下的上、下风侧桥颤振临界风速、气动导数、以及涡振振幅、起振风速、风速锁定区问、斯脱罗哈数等参数的影响规律以及对这种气动干扰效应的重要性有了较为全面的感性认识,从中可总结出以下结论:
(1)气动干扰效应使得平行双幅桥的颤振临界风速明显降低,气动导数曲线由递减向递增变化的转折点均大幅度提前,并且3度风攻角下的平行双幅桥下风侧桥梁的颤振临界风速最低,比单幅桥的颤振临界风速降低了约17%。
(2)不同风攻角下,气动干扰效应对平行双幅桥的涡振振幅影响大小不同,以3度风攻角下的影响最大,0度风攻角下影响次之,-3度风攻角下影响最小。总体而言,双幅桥的涡振振幅显著地大于单幅桥,而其中又以下风侧桥的涡激共振振幅最大。
(3)与单幅桥相比,气动干扰效应使平行双幅桥的涡振起振风速降低、风速锁定区间变长,斯脱罗哈数变大,发生涡激共振的概率增加,而其中又以下风侧桥发生涡激共振的概率最高。














